Persamaan Bernoulli

HUKUM BERNOULLI.

Hukum Bernoulli merupakan persamaan pokok hidrodinamika untuk fluida mengalir dengan arus streamline. Di sini berlaku hubungan antara tekanan, kecepatan alir dan tinggi tempat dalam satu garis lurus. Hubungan tersebut dapat dijelaskan sebagai berikut :

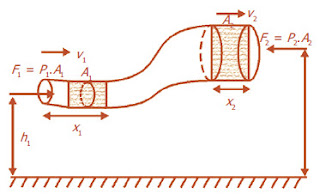
Perhatikan gambar tabung alir a-c pada gambar. Jika tekanan P₁ tekaopan pada penampang A₁, dari fluida di sebelah kirinya, maka gaya yang dilakukan terhadap penampang di a adalah P₁.A₁, sedangkan penampang di c mendapat gaya dari fluida dikanannya sebesar P₂.A₂, di mana P₂ adalah tekanan terhadap penampang di c ke kiri. Dalam waktu Dt detik dapat dianggap bahwa penampang a tergeser sejauh v₁. Dt dan penampang c tergeser sejauh v₂. Dt ke kanan. Jadi usaha yang dilakukan terhadap a adalah : P₁.A₁.v₁. Dt sedangkan usaha yang dilakukan pada c sebesar : - P₂.A₂.v₂. Dt

Jadi usaha total yang dilakukan gaya-gaya tersebut besarnya :

                        W_tot = (P₁.A₁.v₁ - P₂.A₂.v₂) Dt

Dalam waktu Dt detik fluida dalam tabung alir a-b bergeser ke c-d dan mendapat tambahan energi sebesar :

                        E_mek =  D_Ek + D_Ep

                       E_mek = ( ½ m . v₂² – ½ m. v₁²) + (mgh₂ – mgh₁)

                                 = ½ m (v₂² – v₁²) + mg (h₂ – h₁)

Keterangan  : m = massa fluida dalam a-b = massa fluida dalam c-d.

                        h₂-h₁ = beda tinggi fluida c-d dan a-b

Karena m menunjukkan massa fl;uida di a-b dan c-d yang sama besarnya, maka m dapat dinyatakan :

                                   m =  r.A₁.v₁. Dt   =  r.A₂.v₂. Dt

Menurut Hukum kekekalan Energi haruslah :

                                        W_tot = E_mek

Dari persamaan-persaman di atas dapat dirumuskan persaman :

                   P_1m/r + ½ m.v₁² + mgh₁ = P_{2 m/}r + ½ m.v₂² + mgh₂

Suku-suku persamaan ini memperlihatkan dimensi USAHA.

Dengan membagi kedua ruas dengan m/r maka di dapat persamaan :

                   P₁ + ½ r.v₁² + r g h₁ = P₂ + ½ r.v₂² + r g h₂

Suku-suku persamaan di atazs memperlihatkan dimensi TEKANAN.

Keterangan :

P₁ dan P₂ = tekanan yang dialami oleh fluida

v₁ dan v₂ = kecepatan alir fluida

h₁ dan h₂ = tinggi tempat dalam satu garis lurus

              r = Massa jenis fluida

              g = percepatan grafitasI