Kecepatan

Persamaan Gerak

draf soal UAS Fisika2

Ø Draf soal UAS Fisika 2

1. Apabila kita mengerem sepeda motor berarti kita memberikan . . . .

2.   Suatu besaran hasil kali antara massa dengan kecepatan disebut : . . . .

3. Orang naik sampan kemudian orang melompat ke belakang  maka kecepatan sampan akan . . . .

4.    Orang mendorong mobil dengan gaya 1.000 N selama 5 sekon maka orang tersebut akan memberikan impuls yang besarnya . . . .

5. Tanah liat massa 50 gr dilemparkan dengan kecepatan 40 m/s pada balok massa 950 gr diam di lantai kemudian tanah liat menempel pada balok , maka kecepatan balok menjadi  . . .

6.   Sebuah bola besi massa 4 kg bergerak ke kanan dengan kecepatan 10 m/s menumbuk bola      

     kedua dengan massa 1 kg bergerak kiri dengan kecepatan 8 m/s jika tumbukan lenting sebagian dengan koefisien ristitusi 0,5 maka kecepatan bola 4 kg tersebut adalah….m/s

7. Bola A massa 2 kg bergerak dengan kelajuan 8 m/s  menumbuk bola B massa 3 kg yang bergerak dengan kelajuan 5 m/s dengan  arah yang sama  terjadi tumbukan  lenting sempurna . kecepatan bola 2 kg  akan menjadi . . . .
8. Bola dijatuhkan dari ketinggian  16 m kemudian memantul mencapai ketinggian 4 m maka koefisien ristitusi tumbukan tersebut adalah  . . . .
9. Besaran yang didapatkan dari jumlah MR² adalah  . . . .
10. Batang silinder diputar dengan poros melalui pusat silinder besarnya momen inersia . . . .
11. Gaya 8 Newton bekerja pada batang yang memungkinkan berotasi titik tangkap gaya dengan pusat rotasi 50 cm arah gaya membentuk sudut 60⁰ maka besarnya torsi gaya tersebut adalah  . . . .
12. Pasangan dua gaya 20 N yang sama besar dan berlawanan arah terpisah lengan dengan panjang 1,5 m besarnya momen kopel gaya tersebut adalah . . . .
13. Titik tangkap resultan gaya berat dinamakan . . . .
14. Seorang penari balet yang memutar tubuhnya supaya putarannya semakin cepat maka penari balet akan melakukan  . . . .
15. Titik berat kerucut pejal dengan tinggi 20 cm luas alas 6 cm²   adalah  . . . dari alas.
16. Perbedaan antara keseimbangan titik dengan keseimbangan benda tegar  . . . .
17. Pusat massa dan pusat berat dari dua buah benda tidak dalam satu titik dapat terjadi jika . . . .
18. Analisa gambar di bawah

Keseimbangan benda di atas batang massa 6 kg panjang 5 m bersandar pada dinding yang licin, ujung lain 3 m dari dinding, jika batang tepat akan menggeser maka koefisien gesekan antara batang  dengan lantai adalah  . . . .

19. Keseimbangan labil dapat terjadi pada suatu benda mendapatkan gaya, kemudian gaya dihilangkan jika diamati yang terjadi adalah  . . . .
20. Bola menggelinding tanpa tergelincir maka gerakan yang dilakukan bola adalah . . . .
21. Besaran fisika yang merupatan hasil bagi antara gaya normal (tegak lurus ) yang bekerja pada suatu benda dengan luas bidang permukaan tempat gaya bekerja  disebut.
22. Apabila kita menyiram tanaman menggunakan selang plastik kemudian panjang nya kurang maka dengan langkah mengecilkan pipa  konsep tersebut adalah konsep  . . . .
23. Air dialirkan melalui pipa yang berbeda luas penampangnya, jika perbandingan jari jari luas penampang pipa, 2 : 1 maka kecepatan aliran akan terjadi dengan perbandingan . . . .
24. Sebuah bak  air  tingginya 30 cm dari tanah diisi penuh dengan air. Sebuah katub (kran)  berada 20 cm di bawah permukaan air dalam tangki tersebut.

      Ketika katub dibuka, laju  semburan air adalah... .

25. Persamaan Bernoulli diformulasikan : p + ρgh + ½ ρv² = C. Satuan dari C adalah....
26. Penerapan asas Bernoulli dalam kehidupan sehari-hari dapat ditemukan pada alat-alat berikut ini, kecuali . . . .
27. Mobil massa 1000 kg mula-mula diam kemudian didorong dengan gaya 400 N selama 10 s tentukan kecepatan mobil setelah 10 s tersebut.?
28. Dua buah kelereng A dan B massanya sama kelereng A bergerak dengan kecepatan 5 ms^-1 menumbuk kelereng B diam . jika terjadi tumbukan lenting sebagian dengan koefisien ristitusi 0,6 maka tentukan kecepatan kelereng A dan B setelah tumbukan. ?
29. Bola pejal massa 2 kg jari-jari 10 cm menggelinding dilantai tentukan momen inersia bola tersebut ?
30. Orang massa 50 kg bejalan dari A menuju C Jika massa batang homogen  AC 10 kg batang panjang 5 m  sedang jarak AB 4 m jarak terjauh dari B supaya batang masih tetap seimbang ?
31. Sebuah pesawat terbang bergerak dengan kecepatan tertentu sehingga udara yang melalui bagian atas sayap 320 m/s dan bagian bawah sayap 290 m/s sedangkan luas sayap 50 m² tentukan gaya angkat sayap tersebut jika massa jenis udara 1,3 kg/m³

Persamaan Bernoulli

HUKUM BERNOULLI.

Hukum Bernoulli merupakan persamaan pokok hidrodinamika untuk fluida mengalir dengan arus streamline. Di sini berlaku hubungan antara tekanan, kecepatan alir dan tinggi tempat dalam satu garis lurus. Hubungan tersebut dapat dijelaskan sebagai berikut :

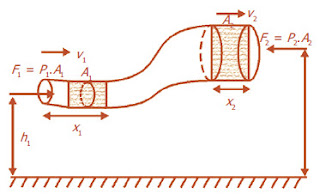
Perhatikan gambar tabung alir a-c pada gambar. Jika tekanan P₁ tekaopan pada penampang A₁, dari fluida di sebelah kirinya, maka gaya yang dilakukan terhadap penampang di a adalah P₁.A₁, sedangkan penampang di c mendapat gaya dari fluida dikanannya sebesar P₂.A₂, di mana P₂ adalah tekanan terhadap penampang di c ke kiri. Dalam waktu Dt detik dapat dianggap bahwa penampang a tergeser sejauh v₁. Dt dan penampang c tergeser sejauh v₂. Dt ke kanan. Jadi usaha yang dilakukan terhadap a adalah : P₁.A₁.v₁. Dt sedangkan usaha yang dilakukan pada c sebesar : - P₂.A₂.v₂. Dt

Jadi usaha total yang dilakukan gaya-gaya tersebut besarnya :

                        W_tot = (P₁.A₁.v₁ - P₂.A₂.v₂) Dt

Dalam waktu Dt detik fluida dalam tabung alir a-b bergeser ke c-d dan mendapat tambahan energi sebesar :

                        E_mek =  D_Ek + D_Ep

                       E_mek = ( ½ m . v₂² – ½ m. v₁²) + (mgh₂ – mgh₁)

                                 = ½ m (v₂² – v₁²) + mg (h₂ – h₁)

Keterangan  : m = massa fluida dalam a-b = massa fluida dalam c-d.

                        h₂-h₁ = beda tinggi fluida c-d dan a-b

Karena m menunjukkan massa fl;uida di a-b dan c-d yang sama besarnya, maka m dapat dinyatakan :

                                   m =  r.A₁.v₁. Dt   =  r.A₂.v₂. Dt

Menurut Hukum kekekalan Energi haruslah :

                                        W_tot = E_mek

Dari persamaan-persaman di atas dapat dirumuskan persaman :

                   P_1m/r + ½ m.v₁² + mgh₁ = P_{2 m/}r + ½ m.v₂² + mgh₂

Suku-suku persamaan ini memperlihatkan dimensi USAHA.

Dengan membagi kedua ruas dengan m/r maka di dapat persamaan :

                   P₁ + ½ r.v₁² + r g h₁ = P₂ + ½ r.v₂² + r g h₂

Suku-suku persamaan di atazs memperlihatkan dimensi TEKANAN.

Keterangan :

P₁ dan P₂ = tekanan yang dialami oleh fluida

v₁ dan v₂ = kecepatan alir fluida

h₁ dan h₂ = tinggi tempat dalam satu garis lurus

              r = Massa jenis fluida

              g = percepatan grafitasI

kisi uas

Kisi Uas Fisika 2 2016

fluida bergerak

FLUIDA BERGERAK

ALIRAN FLUIDA

Di dalam geraknya pada dasarnya dibedakan dalam 2 macam, yaitu :

Aliran laminar / stasioner / streamline.

Aliran turbulen

Suatu aliran dikatakan laminar / stasioner / streamline bila :

Setiap partikel yang melalui titik tertentu selalu mempunyai lintasan (garis arus) yang tertentu pula.

Partikel-partikel yang pada suatu saat tiba di K akan mengikuti lintasan yang terlukis pada gambar di bawah ini. Demikian partikel-partikel yang suatu saat tiba di L dan M.

Kecepatan setiap partikel yang melalui titik tertentu selalu sama. Misalkan setiap partikel yang melalui K selalu mempunyai kecepatan v_K.

Aliran yang tidak memenuhi sifat-sifat di atas disebut : ALIRAN TURBULEN.

 

Pembahasan dalam bab ini di batasi pada fluida ideal, yaitu fluida yang imkompresibel dan bergerak tanpa mengalami gesekan dan pada aliran stasioner.

DEBIT.

Fluida mengalir dengan kecepatan tertentu, misalnya v meter per detik. Penampang tabung alir seperti terlihat pada gambar di atas berpenampang A, maka yang dimaksud dengan DEBIT FLUIDA adalah volume fluida yang mengalir persatuan waktu melalui suatu pipa dengan luas penampang A dan dengan kecepatan v.

                    Q = V/t    atau  Q = A . v

dengan satuan m3/s

Q    = debit fluida dalam satuan SI  m³/det

Vol = volume fluida                         m³

A    = luas penampang tabung alir    m²

V    = kecepatan alir fluida               m/det

Jadi :                                        A₁.v₁  =  A₂.v₂

Persamaan ini disebut : Persamaan KONTINUITAS

A.v yang merupakan debit fluida sepanjang tabung alir selalu konstan (tetap sama nilainya), walaupun A dan v masing-masing berbeda dai tempat yang satu ke tempat yang lain. Maka disimpulkan :

                                     Q =  A₁.v₁  =  A₂.v₂  = konstan

Hukum Archimedes

Hukum Archimedes

Hukum Archimedes mempelajari tentang gaya ke atas yang dialami oleh benda apabila berada dalam fluida. Benda-benda yang dimasukkan pada fluida seakan-akan  mempunyai berat yang lebih kecil daripada saat berada di luar fluida. Misalnya, batu terasa lebih ringan ketika berada di dalam air dibandingkan ketika berada di udara.

Berat di dalam air sesungguhnya tetap, tetapi air melakukan gaya yang arahnya ke atas. Hal ini menyebabkan berat batu akan berkurang, sehingga batu terasa lebih ringan. Berdasarkan peristiwa di atas dapat disimpulkan bahwa berat benda di dalam air besarnya:

Contoh Soal